Resources
Part III: A Guide to Installed Gain | Control Valve Sizing
Submitted by Jon Monsen Ph.D., PE // Flow Control Network Magazine
In order to get good control with stability throughout the full range of required flow rates, one must use a control valve that has an installed flow characteristic that is linear, or at least as close to linear as possible in most systems. This was discussed in detail in Part I of this series in the February issue (pages 29–32). It is often difficult to compare the control capability of two valves with less than perfectly linear installed characteristics by simply studying their installed characteristic graphs, and one can learn more about how well they will control a particular system by examining their installed gain.
Control Valve Installed Gain
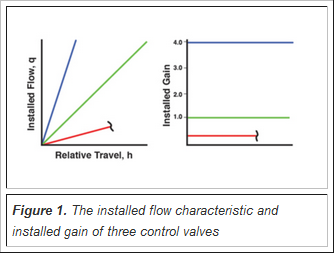 The left graph in Figures 1 and 2 is a control valve’s hypothetical installed flow characteristic, and the right graph is the corresponding installed gain. The gain of a device is defined as the ratio of the change in output to the corresponding change in input. In the case of a control valve, the output is the flow in the system (q) and the input is valve travel (h), meaning its installed gain is defined as: Gain = Δq/Δh. The graphical interpretation of the installed gain is the SLOPE of the installed flow characteristic, and the mathematical interpretation is that the installed gain is the first derivative of the installed flow characteristic.
The left graph in Figures 1 and 2 is a control valve’s hypothetical installed flow characteristic, and the right graph is the corresponding installed gain. The gain of a device is defined as the ratio of the change in output to the corresponding change in input. In the case of a control valve, the output is the flow in the system (q) and the input is valve travel (h), meaning its installed gain is defined as: Gain = Δq/Δh. The graphical interpretation of the installed gain is the SLOPE of the installed flow characteristic, and the mathematical interpretation is that the installed gain is the first derivative of the installed flow characteristic.
The green line in the left graph of Figure 1 represents an ideal linear installed flow characteristic where the ideal linear installed characteristic is a straight line, and changes in relative valve travel (Δh) cause equal changes in relative flow (Δq). In the figure, a change in valve position of 1 percent causes a change in flow of 1 percent. Because the slope of the green line is constant, it follows that this valve’s installed gain will be constant, and because a change in position of 1 percent causes a change in relative flow of 1 percent, its installed gain is 1, (gain = 1%/1% = 1.0). So just as the green line in the installed characteristic graph represents the ideal linear installed flow characteristic, the green line in the installed gain graph with a constant value of 1.0 represents the ideal installed gain.
It’s impossible to get the exact ideal installed characteristic and installed gain because: (1) real valves do not have exact linear or equal percentage inherent characteristics; and (2) the interaction between the equal percentage inherent characteristic and the system characteristic do not exactly cancel each other. However, one strives to get as close as possible. This is why the perfectly linear installed characteristic and the constant installed gain of 1.0 are the benchmarks.
In Figure 1 there are two other valves with straight line installed flow characteristics. One has a very steep slope and the other a very shallow slope.
The valve with the blue graph, whose installed characteristic has a steep slope, is a very sensitive valve. Its installed gain graph has a constant, but large value.
The valve with the red graph, whose installed characteristic has a shallow slope, is a very insensitive valve. (In the figure, only the portion of the valve’s characteristic that we are concerned with is shown.) Its gain graphs as a constant, but small value. Neither of these valves would make a very good control valve. The low gain valve would not make a good control valve because when the valve stem moves, the flow hardly changes at all. A control valve that, when it moves, does not change the flow is not much of a control valve. The valve with the steep slope has a very high gain, meaning that small changes in valve position cause very large changes in flow. It is less obvious why this valve would not be a good control valve. When two parts (such as a ball and a seat, or a valve shaft and packing) are in contact with each other, they exhibit two kinds of friction. When the parts are not moving, they tend to stick together and the friction is high. When they are moving the friction becomes much lower. The interaction between static and dynamic friction makes it very difficult to position a valve exactly where it needs to be. From the definition of gain, the change in flow is equal to the change in position multiplied by the installed gain (Δq = Δh * Gain). If the high gain valve (installed gain of 4) could only be positioned in 1 percent increments, the most accurately that flow could be controlled would be in 4 percent increments, which might not be accurate enough
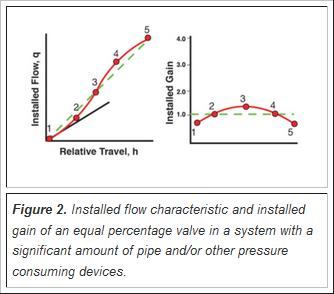 Understanding the meaning of installed gain, how does one apply this concept to an equal percentage valve installed in a system with a lot of pipe (and/or other pressure-consuming elements), where the installed characteristic is nearly linear but slightly “S” shaped, as shown in the left graph of Figure 2? The dashed lines represent the hypothetical ideal linear installed characteristic and the resulting ideal installed gain with a constant value of 1.0. Here the shape of the installed characteristic graph is constantly changing, and its slope is as well. Consider the instantaneous slope (and thus the installed gain) at several points.
Understanding the meaning of installed gain, how does one apply this concept to an equal percentage valve installed in a system with a lot of pipe (and/or other pressure-consuming elements), where the installed characteristic is nearly linear but slightly “S” shaped, as shown in the left graph of Figure 2? The dashed lines represent the hypothetical ideal linear installed characteristic and the resulting ideal installed gain with a constant value of 1.0. Here the shape of the installed characteristic graph is constantly changing, and its slope is as well. Consider the instantaneous slope (and thus the installed gain) at several points.
At Point 1, a line has been drawn that is tangent to the installed characteristic to represent the instantaneous slope of the installed characteristic (and thus the installed gain) at Point 1. This tangent is not as steep as the ideal linear installed characteristic, and therefore the gain is less than the ideal 1.0. A point has been placed on the installed gain graph (Point 1) that is less than the ideal gain of 1.0.
At Point 2, if one were to draw a tangent to the installed characteristic graph, it would be parallel to the ideal linear graph. This means, at Point 2, the instantaneous gain is 1.0, and a corresponding Point 2 is placed on the installed gain graph at a gain of 1.0.
If one continues drawing tangent lines at Points 3, 4 and 5, the corresponding Points 3, 4 and 5 on the installed gain graph are achieved.
Typically, the installed characteristic and installed gain graphs of equal percentage valves in systems with a lot of pipe (and/or other pressure consuming elements), which is the most common case, will have shapes similar to those in Figure 2, but not necessarily as symmetrical as shown in the figure.
Control Valve Installed Gain Recommendations
Below are recommendations (and the rules that Nelprof, the Metso control valve sizing and selection software, uses when selecting the best valve size for an application) for gain magnitude and variation.
Within the specified control range:
Typically, if the gain changes by not much more than a 2-to-1 ratio, it will be possible to come up with one set of PID tuning parameters that will result in good control and stability throughout the required flow range. As the variation in gain within the specified flow range becomes larger, it will become more difficult to tune the system for both stable and good control.
When selecting the best valve out of several that meet the first three criteria, criteria 4 and 5 should be considered. The gain should be as constant as possible. The more constant the gain, the more aggressive the PID tuning can be without the danger of instability. The gain should also be as close to 1 as possible. Usually, when comparing the installed gain of different valves for the same application, as the gain becomes more constant, it also comes closer to 1.
Selecting the Best Valve Based On Installed Gain
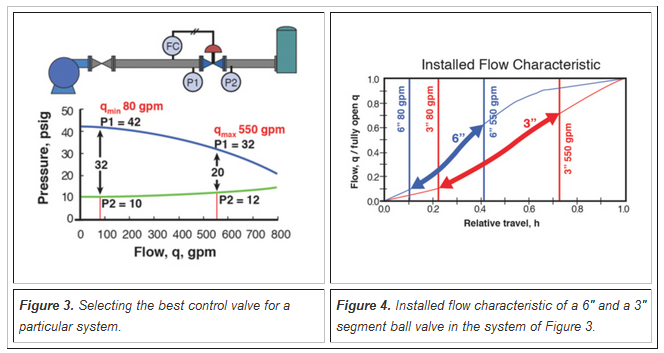 There is a control valve sizing program which, based on a database of actual valve inherent characteristics, along with some user-supplied information about how the system pressure drop changes with flow, can calculate and graph the installed flow characteristic of a particular type and size valve in its particular system. Next, the program calculates the first derivative of the installed flow characteristic and graphs it as the installed gain. In order for the program to define the process model, at least two flow points (maximum and minimum required flow) are required along with the associated values of pressure upstream of the control valve, P1, and the pressure drop across the control valve, ΔP.
There is a control valve sizing program which, based on a database of actual valve inherent characteristics, along with some user-supplied information about how the system pressure drop changes with flow, can calculate and graph the installed flow characteristic of a particular type and size valve in its particular system. Next, the program calculates the first derivative of the installed flow characteristic and graphs it as the installed gain. In order for the program to define the process model, at least two flow points (maximum and minimum required flow) are required along with the associated values of pressure upstream of the control valve, P1, and the pressure drop across the control valve, ΔP.
Using this software one can demonstrate how an analysis of installed gain can help select the best control valve for a particular system. The demonstration is based on the system shown in Figure 3. The graph in Figure 3 shows how P1, P2 and ΔP vary with flow as modeled by the software. The goal is to select a valve whose installed gain does the best job of meeting the installed gain recommendations given above. For this example, things like choked flow, noise and velocity do not affect the selection, allowing one to concentrate on installed gain.
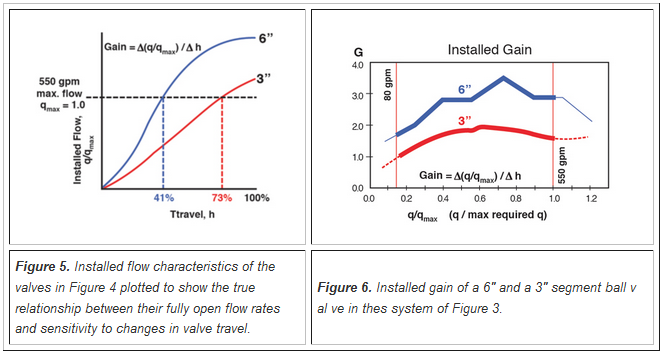 Figure 4 shows the installed flow characteristics of two valves being considered for the application, a 6” segment ball valve and a 3” segment ball valve. Emphasis has been added to the portions of the installed flow graphs that are within the specified flow range of 80 to 550 gallons per minute. Because segment ball valves have an inherent equal percentage flow characteristic and because the system is one where valve pressure drop decreases with increasing flow, it is not surprising that the installed flow characteristics are very nearly linear (especially within the specified flow range). This computer-generated graph shows how linear the installed characteristics are and how much safety factor is at each end of the required flow range. However, because the vertical scale is normalized to show actual flow divided by the fully open flow for each valve, when comparing several valves for the same application, one cannot see the differences in the steepness (slope) of the graph and thus the sensitivity to changes in valve position. If the data in Figure 4 were plotted on a GPM scale, instead of flow divided by fully open flow, it would look like Figure 5 where the relative steepness of different valves can be clearly seen. The program uses a graph like Figure 5, where the gain is calculated based on the maximum required flow, qmax, that is Gain =Δ (q/qmax) / Δh. Note that this graph on a GPM scale is not visible to the user.
Figure 4 shows the installed flow characteristics of two valves being considered for the application, a 6” segment ball valve and a 3” segment ball valve. Emphasis has been added to the portions of the installed flow graphs that are within the specified flow range of 80 to 550 gallons per minute. Because segment ball valves have an inherent equal percentage flow characteristic and because the system is one where valve pressure drop decreases with increasing flow, it is not surprising that the installed flow characteristics are very nearly linear (especially within the specified flow range). This computer-generated graph shows how linear the installed characteristics are and how much safety factor is at each end of the required flow range. However, because the vertical scale is normalized to show actual flow divided by the fully open flow for each valve, when comparing several valves for the same application, one cannot see the differences in the steepness (slope) of the graph and thus the sensitivity to changes in valve position. If the data in Figure 4 were plotted on a GPM scale, instead of flow divided by fully open flow, it would look like Figure 5 where the relative steepness of different valves can be clearly seen. The program uses a graph like Figure 5, where the gain is calculated based on the maximum required flow, qmax, that is Gain =Δ (q/qmax) / Δh. Note that this graph on a GPM scale is not visible to the user.
Figure 6 shows the installed gain of the same two valves. Again, emphasis has been added to the portion of the graphs that are within the specified flow range of 80 GPM to 550 GPM. Examining the two graphs, it is immediately clear that the 3” valve is the best choice because it meets all of the above installed gain recommendations, and the 6” valve does not. The 6” valve has a maximum gain of about 3.5. This means at that point, a 1 percent valve position error would cause a 3.5 percent flow error. In contrast, a similar position error with the 3” valve would result in a 2 percent flow error. The change in gain within the specified flow range is about 2-to-1 for both valves. The gain of the 3” valve is clearly closer to 1 than the 6” valve. Had a 4” valve been analyzed, it would have been found to be better than the 6” valve, but not as good as the 3” valve. Note that on the gain graph, 1.0 on the q/qmaz axis will always be the maximum required flow.
NOTE: The program cannot actually show the results for two valves at one time. The graphs shown above were produced by combining the results from the two calculations into a single graph. When using the sizing program, it is possible to quickly step through the graphs for each of several valves to easily compare them.
Read:
Part I: An Insider's Guide to Control Valves & Process Control
Part II: An Insider’s Guide to Control Valves & Process Variability
Part IV: Keys to Effective Valve Sizing & Selection
Control Valve Installed Gain

The green line in the left graph of Figure 1 represents an ideal linear installed flow characteristic where the ideal linear installed characteristic is a straight line, and changes in relative valve travel (Δh) cause equal changes in relative flow (Δq). In the figure, a change in valve position of 1 percent causes a change in flow of 1 percent. Because the slope of the green line is constant, it follows that this valve’s installed gain will be constant, and because a change in position of 1 percent causes a change in relative flow of 1 percent, its installed gain is 1, (gain = 1%/1% = 1.0). So just as the green line in the installed characteristic graph represents the ideal linear installed flow characteristic, the green line in the installed gain graph with a constant value of 1.0 represents the ideal installed gain.
It’s impossible to get the exact ideal installed characteristic and installed gain because: (1) real valves do not have exact linear or equal percentage inherent characteristics; and (2) the interaction between the equal percentage inherent characteristic and the system characteristic do not exactly cancel each other. However, one strives to get as close as possible. This is why the perfectly linear installed characteristic and the constant installed gain of 1.0 are the benchmarks.
In Figure 1 there are two other valves with straight line installed flow characteristics. One has a very steep slope and the other a very shallow slope.
The valve with the blue graph, whose installed characteristic has a steep slope, is a very sensitive valve. Its installed gain graph has a constant, but large value.
The valve with the red graph, whose installed characteristic has a shallow slope, is a very insensitive valve. (In the figure, only the portion of the valve’s characteristic that we are concerned with is shown.) Its gain graphs as a constant, but small value. Neither of these valves would make a very good control valve. The low gain valve would not make a good control valve because when the valve stem moves, the flow hardly changes at all. A control valve that, when it moves, does not change the flow is not much of a control valve. The valve with the steep slope has a very high gain, meaning that small changes in valve position cause very large changes in flow. It is less obvious why this valve would not be a good control valve. When two parts (such as a ball and a seat, or a valve shaft and packing) are in contact with each other, they exhibit two kinds of friction. When the parts are not moving, they tend to stick together and the friction is high. When they are moving the friction becomes much lower. The interaction between static and dynamic friction makes it very difficult to position a valve exactly where it needs to be. From the definition of gain, the change in flow is equal to the change in position multiplied by the installed gain (Δq = Δh * Gain). If the high gain valve (installed gain of 4) could only be positioned in 1 percent increments, the most accurately that flow could be controlled would be in 4 percent increments, which might not be accurate enough

At Point 1, a line has been drawn that is tangent to the installed characteristic to represent the instantaneous slope of the installed characteristic (and thus the installed gain) at Point 1. This tangent is not as steep as the ideal linear installed characteristic, and therefore the gain is less than the ideal 1.0. A point has been placed on the installed gain graph (Point 1) that is less than the ideal gain of 1.0.
At Point 2, if one were to draw a tangent to the installed characteristic graph, it would be parallel to the ideal linear graph. This means, at Point 2, the instantaneous gain is 1.0, and a corresponding Point 2 is placed on the installed gain graph at a gain of 1.0.
If one continues drawing tangent lines at Points 3, 4 and 5, the corresponding Points 3, 4 and 5 on the installed gain graph are achieved.
Typically, the installed characteristic and installed gain graphs of equal percentage valves in systems with a lot of pipe (and/or other pressure consuming elements), which is the most common case, will have shapes similar to those in Figure 2, but not necessarily as symmetrical as shown in the figure.
Control Valve Installed Gain Recommendations
Below are recommendations (and the rules that Nelprof, the Metso control valve sizing and selection software, uses when selecting the best valve size for an application) for gain magnitude and variation.
Within the specified control range:
- Gain > 0.5
- Gain < 3.0
- Gain (max) / Gain (min) < 2.0
- As constant as possible
- As close to 1.0 as possible
Typically, if the gain changes by not much more than a 2-to-1 ratio, it will be possible to come up with one set of PID tuning parameters that will result in good control and stability throughout the required flow range. As the variation in gain within the specified flow range becomes larger, it will become more difficult to tune the system for both stable and good control.
When selecting the best valve out of several that meet the first three criteria, criteria 4 and 5 should be considered. The gain should be as constant as possible. The more constant the gain, the more aggressive the PID tuning can be without the danger of instability. The gain should also be as close to 1 as possible. Usually, when comparing the installed gain of different valves for the same application, as the gain becomes more constant, it also comes closer to 1.
Selecting the Best Valve Based On Installed Gain

Using this software one can demonstrate how an analysis of installed gain can help select the best control valve for a particular system. The demonstration is based on the system shown in Figure 3. The graph in Figure 3 shows how P1, P2 and ΔP vary with flow as modeled by the software. The goal is to select a valve whose installed gain does the best job of meeting the installed gain recommendations given above. For this example, things like choked flow, noise and velocity do not affect the selection, allowing one to concentrate on installed gain.

Figure 6 shows the installed gain of the same two valves. Again, emphasis has been added to the portion of the graphs that are within the specified flow range of 80 GPM to 550 GPM. Examining the two graphs, it is immediately clear that the 3” valve is the best choice because it meets all of the above installed gain recommendations, and the 6” valve does not. The 6” valve has a maximum gain of about 3.5. This means at that point, a 1 percent valve position error would cause a 3.5 percent flow error. In contrast, a similar position error with the 3” valve would result in a 2 percent flow error. The change in gain within the specified flow range is about 2-to-1 for both valves. The gain of the 3” valve is clearly closer to 1 than the 6” valve. Had a 4” valve been analyzed, it would have been found to be better than the 6” valve, but not as good as the 3” valve. Note that on the gain graph, 1.0 on the q/qmaz axis will always be the maximum required flow.
NOTE: The program cannot actually show the results for two valves at one time. The graphs shown above were produced by combining the results from the two calculations into a single graph. When using the sizing program, it is possible to quickly step through the graphs for each of several valves to easily compare them.
Read:
Part I: An Insider's Guide to Control Valves & Process Control
Part II: An Insider’s Guide to Control Valves & Process Variability
Part IV: Keys to Effective Valve Sizing & Selection
Click Here to Download PDF
A lesson for me is that I need to involve you earlier in the program.
You were tireless in your support and it will not be forgotten!
Latest from Valin's Blog
The NIST Chemistry WebBook contains a great deal of information regarding the properties of a broad range of chemicals and is helpful for those who deal with chemical processes.In this article, Jon Monsen has outlined the procedure for finding the actual density of a gas using the WebBook.

